integrating sine and cosine products|6.3: Trigonometric Integrals : Tuguegarao A key idea behind the strategy used to integrate combinations of products and powers of sinx and cosx involves rewriting these expressions as sums and differences of integrals of the form ∫sinjxcosxdx or ∫cosjxsinxdx. After rewriting these integrals, we evaluate them . We would like to show you a description here but the site won’t allow us.
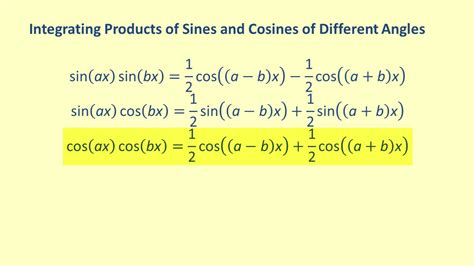
integrating sine and cosine products,A key idea behind the strategy used to integrate combinations of products and powers of sinx and cosx involves rewriting these expressions as sums and differences of integrals of the form ∫sinjxcosxdx or ∫cosjxsinxdx. After rewriting these integrals, we evaluate them .Integrating Products and Powers of sin x and cos x. A key idea behind the strategy used to integrate combinations of products and powers of \(\sin x\) and \(\cos x\) involves .6.3: Trigonometric Integrals Key Idea 11: Integrals Involving Powers of Sine and Cosine. Consider \( \int \sin^mx\cos^nx\ dx\), where \(m,n\) are nonnegative integers. If \(m\) is odd, then .This section looks at integrals involving the product(s) of sine and cosine functions having different linear arguments, e.g. ∫ sin (a x) sin (b x) d x, or ∫ sin 2 (a x) cos (c x) d x. Use .integrating sine and cosine products 8.3: Powers of sine and cosine. Functions consisting of products of the sine and cosine can be integrated by using substitution and trigonometric identities. These . In this section we look at integrals that involve trig functions. In particular we concentrate integrating products of sines and cosines as well as products of secants .Integrating Products and Powers of sin x and cos x. A key idea behind the strategy used to integrate combinations of products and powers of sinx and cosx involves rewriting .Lecture 10: Powers of sin and cos. Integrating non-negative powers of sin and cos. The goal. In this section, we learn how to evaluate integrals of the form. Z. sinnxcosmxdx: .
How to integrate powers of sine and cosine, examples and step by step solutions, free online calculus lectures in videos. Functions consisting of products of the sine and cosine can be integrated by using substitution and trigonometric identities. These can sometimes be tedious, but .integrating sine and cosine products 6.3: Trigonometric Integrals Integrating Products and Powers of sin x and cos x. A key idea behind the strategy used to integrate combinations of products and powers of \(\sin x\) and \(\cos x\) involves rewriting these expressions as sums and differences of integrals of the form \(∫\sin^jx\cos x\,dx\) or \(∫\cos^jx\sin x\,dx\).Odd Power of Sine or Cosine. To integrate an odd power of sine or cosine, we separate a single factor and convert the remaining even power. If the power of cosine is odd (n = 2k + 1), save one cosine .
Integrating Products of Sines and Cosines. This section looks at integrals involving the product(s) of sine and cosine functions having different linear arguments, e.g. ∫ sin (a x) sin (b x) d x, or ∫ sin 2 (a x) cos (c x) d x. Use is made of the following three basic sine and cosine product identities involving different arguments:
We show how to integrate a product of sines and cosines, when either there are an odd number of sines or an odd number of cosines
Let’s begin our study with products of sin x sin x and cos x. cos x. Integrating Products and Powers of sinx and cosx. A key idea behind the strategy used to integrate combinations of products and powers of sin x sin x and cos x cos x involves rewriting these expressions as sums and differences of integrals of the form ∫ sin j x cos x d x .
Well, let's just rewrite this part right over here, leveraging some trig identities. And if this is completely unfamiliar to you, I encourage you to review your trig identities on Khan . We generalize this integral and consider integrals of the form \(\int \sin^mx\cos^nx\ dx\), where \(m,n\) are nonnegative integers. Our strategy for evaluating these integrals is to use the identity \(\cos^2x+\sin^2x=1\) to convert high powers of one trigonometric function into the other, leaving a single sine or cosine term in the integrand.
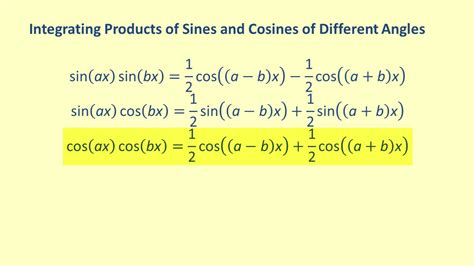
Integrating Products of Sin(x) and Cos(x) If you’re integrating a product of sine and cosine, you will need to use an identity to simplify the function before integrating. For instance, the integral of sin(x)cos(x) can be simplified to .
integrating sine and cosine products|6.3: Trigonometric Integrals
PH0 · Lecture 10: Powers of sin and cos
PH1 · Integrating Products of Sines and Cosines of Different
PH2 · Integrating Products and Powers of sinx and cosx
PH3 · Integrals involving Powers of Sines and Cosines
PH4 · Calculus II
PH5 · 8.3: Powers of sine and cosine
PH6 · 8.2 Powers of sine and cosine
PH7 · 7.2: Trigonometric Integrals
PH8 · 6.3: Trigonometric Integrals
PH9 · 3.2 Trigonometric Integrals